Метод сравнительной статистики при анализе крови
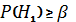
Наиболее
часто встречающейся и достаточно сложной
математико-статистической задачей
является сравнение данных, полученных
в процессе наблюденийилиэкспериментов,
в выборочных совокупностях. Исследователь
старается описать результаты наблюдения
количественными методами и «на выходе»
получает числовой массив тех или иных
доступных ему измерений – вариационный
ряд. Однако, как правило, содержащаяся
в результатах измерений содержательная
информация, имеет гораздо большую
ценность при сравнении ее с аналогичной
информацией, но полученной некоторым
иным образом.
Например,
это может быть ситуация сравнения
опытных данных (когда мы как-то повлияли
на изучаемый объект или явление) с
контрольной
группой, в которой никакого воздействия
на объект наблюдения не было.
Возможно и сравнение двух вариантов
опытов. Возможно сравнение двух серий
наблюдений,
разделенных в пространстве и времени
и т.п.
Допустим,
что удается заметить какие-либо численные
различия в характеристиках сравниваемых
рядов. Первым делом возникает вопрос:
какова вероятность, что эти различия
неслучайны и будут систематически
повторяться в дальнейшем при воспроизведении
условий эксперимента или наблюдения,
т.е. выявленные различия являются
статистически
значимыми.
Выбор
подходящего метода сравнения выборочных
совокупностей определяется несколькими
факторами: характером сравниваемых
признаков (качественные или количественные),
числом сопоставляемых групп, зависимостью
или независимостью выборок, а также
видом распределения признака.
Выборки
являются независимыми,
если набор объектов исследования в
каждую из групп осуществлялся независимо
от того, какие объекты исследования
включены в другую группу. Так, в частности,
происходит при рандомизации, когда
распределение объектов происходит
случайным образом. Примером сравнения
независимых выборок может служить
сопоставление данных анализа крови в
группе пациентов с аналогичными
показателями в группе здоровых.
Группы
являются зависимыми
(связанными) в
динамических исследованиях, когда
изучаются одни и те же объекты в разные
моменты времени. Например, показатели
анализа крови у одних и тех же пациентов
до и после лечения.
От
вида распределения и типа исследуемого
признака зависит выбор подходящего
математико-статистического критерия.
Критерии делятся на два типа –
параметрические
и
непараметрические.
Параметрические
критерии –
критерии, основанные на оценке параметров
распределения, к которым относятся
среднее арифметическое, среднеквадратическое
отклонение, дисперсия. Они
применимы
только в том случае, если численные
данные подчиняются нормальному
распределению.
Если распределение отличается от
нормального, то следует пользоваться
так называемыми непараметрическими
критериями.
Непараметрические
критерии не
основаны на оценке параметров распределения
и вообще не
требуют, чтобы данные подчинялись
какому-то определенному типу распределения.
Непараметрические критерии дают более
грубые оценки, чем параметрические, но
являются более универсальными. А
параметрические методы более точны, но
лишь в случае, если правильно определено
распределение совокупности.
Перед
тем как перейти к рассмотрению
статистических критериев, введем понятия
нулевой и
альтернативной
гипотез,
которые нам потребуются в дальнейшем.
На
каждом шаге процесса анализа данных
выдвигаются две
гипотезы.Первая
обозначается
и называется нулевой
гипотезой.
Вторая
гипотеза обозначается ![]()
и носит название
альтернативной,т.е.
противоположной по смыслу. Под «нулевой
гипотезой» подразумевается допущение
об отсутствии того или иного интересующего
исследователя события, явления или
эффекта, а под «альтернативной» – о его
наличии. Обе гипотезы, как бы они не были
сформулированы, обязательно должны
иметь взаимоисключающеесодержание.
Нулевая
гипотезане
может быть
отвергнута,
если ее вероятность окажется выше некого
наперед заданного уровня
α, достаточно
близкого к 0, т.е. ![]() .
.
Эта величина
α носит
название уровень
значимости нулевой гипотезы.
Альтернативная
гипотеза ![]() может
может
быть принята
лишь в том случае, если ее вероятность
достигнет некого наперед заданного
уровня
β или
превзойдет его, т.е. ![]() .
.
Эта величина β – уровень
доверительной вероятности.
Он соответствует
«уровням безошибочных прогнозов», т.е.
вероятностям 0.95, 0.99 и 0.999 (область
практически достоверных событий).
Соответственно,
α очерчивает
область
практически невозможных событий
с порогами вероятностей 0.05, 0,01 и 0.001.
Поскольку
![]()
и ![]()
– альтернативные гипотезы, то их
суммарная вероятность равна единице.
Следовательно, рост вероятности одной
из гипотез автоматически приводит к
снижению вероятности другой. Например,
если ![]() ,
,
это означает то, что будет выполняться
условие ![]() .
.
И в этом случае нулевая гипотеза может
быть отвергнута как событие практически
невозможное, а альтернативная должна
быть принята как событие практически
достоверное. Если же ![]() ,
,
то ![]() .
.
И в этой ситуации нулевая гипотеза не
может быть отвергнута, а альтернативная
не может быть принята.
Например,
в процессе исследования ставится задача
доказать наличие статистически значимых
различий между результатами наблюдений
в опытной и контрольной группах. Это
значит, что данные, полученные при
применении того или иного статистического
критерия, должны позволить отвергнуть
нулевую гипотезу об отсутствии указанных
различий.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
Прежде чем приступать к выбору статистического критерия, нужно определиться с тем, от чего зависит применение тех или иных статистических методов. Ранее мы уже подразделяли наши данные на количественные и качественные (см. статью «Типы данных»), изучали способы их описания в зависимости от типов признаков и видов распределения (см. статью «Описательная статистика» и «Виды распределений»). Для вариационных рядов, которые имеют нормальное распределение, мы рассчитывали определенные параметры, с помощью которых можно описать вариационный ряд. Для нормального распределения это – средняя величина и стандартное отклонение. В случае распределения, отличного от нормального, используются медиана и интерквартильный интервал, с помощью которых можно было описать большую часть данных.
Определение задачи, которая будет решаться с использованием статистических методов.
До того, как выбирать тот или иной статистический критерий исследователь прежде всего должен определиться, какие именно задачи будут решаться, и какие методы (статистические тесты) для этого будут подбираться.
Как таковые задачи можно разделить на несколько групп:
Предварительные задачи: Описание данных
Само по себе описание данных не является аналитической задачей. Задача описания данных состоит в упорядочивании и компактном представлении данных. Методы описательной статистики напрямую зависит от типа данных, с которым мы имеем дело. Ранее мы уже подразделяли наши данные на количественные и качественные (см. статью «Типы данных»), изучали способы их описания в зависимости от типов признаков и видов распределения (см. статью «Описательная статистика» и «Виды распределений»). Для вариационных рядов, которые имеют нормальное распределение, мы рассчитывали определенные параметры, с помощью которых можно описать вариационный ряд. Для нормального распределения это – средняя величина и стандартное отклонение. В случае распределения, отличного от нормального, используются медиана и интерквартильный интервал, с помощью которых можно было описать большую часть данных. Для качественных данных описание заключается в нахождении частот, долей, пропорций, представление в виде абсолютных и относительных величин.
- Оценка динамики явления — решается прежде всего через инструменты оценки динамических рядов
- Анализ различий между группами (статистическими совокупностями) в зависимости от типа данных и распределения количественных данных, количества и связанности групп может применяться большое количество инструментов. Этот пункт будет изложен в этой статье подробным образом
- Выявление и оценка взаимовлияний в динамике — в зависимости от типа данных и их распределения используются различные методы корелляционного анализа.
- Прогноя явлений — используются линейные и логистические регрессии (возможно, в связке с ROC-analysis), деревья решений, нейронные сети, различные вариантры дискриминативного анализа
- Группировка явлений и выявление общих свойств группы — варианты кластерного анализа.
Выбор статистического критерия для тестирования гипотез о различии групп
Наиболее частой задачей является сравнение статистических совокупностей (групп, выборок) на предмет статистически значимых различий между ними (подробнее см. «Ошибка первого рода, статистическая значимость»). К примеру в результате исследования «случай-контроль» или когортного исследования необходимо сравнить показатели длительности послеоперационного периода, частоты осложнений, функционального состояния импланта и пр.
Алгоритм выбора (Рисунок 1).
- Уточните тип данных (количественные или качественные)
- В случае количественных данных уточните тип распределения (нормальное или отличное от нормального)
- Уточните количество групп сравнения. Важный пункт, о котором часто забывают сравнивать группы 1 раз попарно в случае двух групп и три раза попарно в случае трех не одно и тоже. В данном контексте нужно учитывать увеличение ошибки первого рода в случае множественных сравнений. Для таких ситуаций есть отдельные статистические методы (к примеру вместо т-критерия стьюдента используется дисперсионный анализ).
- Уточните, связан ли группы сравнения между собой (в данном случае речь идет об идентичности единиц наблюдения в группах), т.е. являются ли единицы наблюдения в группах разными носителями признака (независимые или «опыт-контроль»), или это одни и те же пациенты, опрашиваемые, предметы, сопряженные «до и после эксперимента». В зависимости от ответа на этот вопрос меняется логика выбора статистического критерия.
В случае выбора статистического критерия для сравнения количественных данных нужно учитывать распределение признака: является ли оно нормальным или отличным от нормального. В первом случае, как и при описании вариационного ряда, мы будет использовать параметры распределения, отсюда и название этой группы методов: параметрические методы, в случае отличного от нормального распределения следует использовать непараметрические методы.
Параметрические статистические методы
Класс статистических методов, используемых для анализа данных, которые образуют известное распределение (обычно нормальное). Названы так потому, что основываются на оценке параметров (таких как среднее или стандартное отклонение) выборочного распределения интересующей величины.
Непараметрические методы
Непараметрические методы не основываются на оценке параметров (таких как среднее или стандартное отклонение) при описании выборочного распределения интересующей величины. Поэтому эти методы иногда также называются свободными от параметров или свободно распределенными.
Статистические методы с (некоторыми) желательными свойствами, сохраняющимися при относительно слабых допущениях о рассматриваемых генеральных совокупностях. Непараметрические методы позволяют обрабатывать данные «низкого качества» из выборок малого объёма с переменными, про распределение которых мало что или вообще ничего неизвестно.
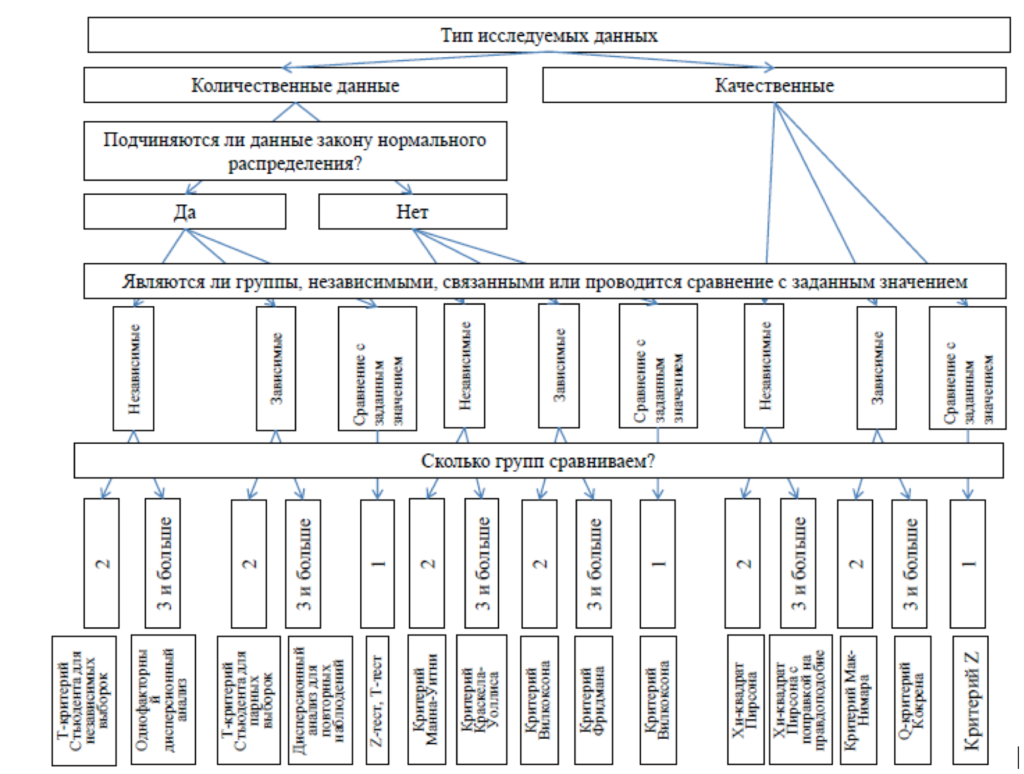
Рисунок 1. Выбор статистического критерия для сравнения статистических совокупностей (По Мильчаков К.С.)
Пример выбора статистического критерия для сравнения статистических совокупностей
Пример 1: Для оценки успешности реабилитации после эндопротезирования коленного сустава было проведено исследование у двух выборок (n1=10; n2=10) на предмет скорости восстановления к сгибанию в колене. В первой выборке оказались люди прошедшие полный курс реабилитации, во второй пациенты, отказавшиеся от услуг реабилитолога. Сделайте статистический вывод о пользе реабилитологического сопровождения на основании представленных данных, прдположим, что данные распределены отличным от нормального образом.
| Группа «Реабилитация», срок в днях | Группа «без реабилитации», срок в днях |
| 22.1 | 32.5 |
| 22.3 | 37.1 |
| 26.2 | 39.1 |
| 29.6 | 40.5 |
| 31.7 | 45.5 |
| 33.5 | 51.3 |
| 38.9 | 52.6 |
| 39.7 | 55.7 |
| 43.2 | 55.9 |
| 43.2 | 57.7 |
Ответ: Тип данных: количественный, непрерывный, распределение: отличное от нормального, количество групп: 2, связанность групп: не связаны. необходимо использовать критерий Манна-Уитни
Пример 2:
При заболеваниях сетчатки повышается проницаемость ее сосудов. Дж. Фишмен и соавт. (G. Fishman et al. Blood-retinal barrier function in patients with cone or cone-rod dystrophy. Arch. Ophthalmol., 104:545—548, 1986) измерили проницаемость сосудов сетчатки у здоровых и у больных с ее поражением. Полученные результаты приведены в таблице. Сделайте вывод о проницаемости сетчатки у больных с дистрофией и относительно здорового контроля.
Проницаемость сосудов сетчатки, мм:
| Здоровые | Больные |
| 0,5 | 1,2 |
| 0,7 | 1,4 |
| 0,7 | 1,6 |
| 1 | 1,7 |
| 1 | 1,7 |
| 1,2 | 1,8 |
| 1,4 | 2,2 |
| 1,4 | 2,3 |
| 1,6 | 2,4 |
| 1,6 | 6,4 |
| 1,7 | 19 |
| 2,2 | 23,6 |
Ответ: Тип данных: количественный, непрерывный, распределение: неизвестно. Количество групп: 2, связанность групп: не связаны.
Необходимо использовать критерий Манна-Уитни или после проверки распределения (в случае нормального распределения величины) использовать т-критерий Стьюдента для несвяазанных совокупностей.
Пример 3:
Бишоп (Т. Bishop. High frequency neural modulation in dentistry. J. Am. Dent. Assoc., 112:176—177, 1986) изучил эффективность высокочастотной стимуляции нерва в качестве обезболивающего средства при удалении зуба. Все больные подключались к прибору, но в одних случаях он работал, в других был выключен. Ни стоматолог, ни больной не знали, включен ли прибор. Позволяют ли следующие данные считать высокочастотную стимуляцию нерва действенным анальгезируюшим средством?
| Прибор включен | Прибор выключен | |
| Боли нет | 24 | 3 |
| Боли есть | 6 | 17 |
Ответ: Тип данных: качественный, абсолютные частоты, количество групп: 2, связанность групп: не связаны.
Необходимо использовать хи-квадрат Пирсона (или точный критерий Фишера).
NB! о выборе статистического критерия
Каждый статистический критерий работает с определенным набором данных и в условиях определенный групп. Аккуратно выбирайте статистические критерии, не упускайте логику выбора и результат Ваших расчетов будет корректным и не вызывающим сомнения о профессиональных статистических рецензентов, как при презентации материала на конференции, сдаче отчета о клиническом исследовании или публикации статьи. Удачи на научном поприще!
Если Вам понравилась статья и оказалась полезной, Вы можете поделиться ею с коллегами и друзьями в социальных сетях:
Источник
Не потеряйте. Подпишитесь и получите ссылку на статью себе на почту.
Деятельность людей во множестве случаев предполагает работу с данными, а она в свою очередь может подразумевать не только оперирование ими, но и их изучение, обработку и анализ. Например, когда нужно уплотнить информацию, найти какие-то взаимосвязи или определить структуры. И как раз для аналитики в этом случае очень удобно пользоваться не только разными техниками мышления, но и применять статистические методы.
Особенностью методов статистического анализа является их комплексность, обусловленная многообразием форм статистических закономерностей, а также сложностью процесса статистических исследований. Однако мы хотим поговорить именно о таких методах, которые может применять каждый, причем делать это эффективно и с удовольствием.
Статистическое исследование может проводиться посредством следующих методик:
- Статистическое наблюдение;
- Сводка и группировка материалов статистического наблюдения;
- Абсолютные и относительные статистические величины;
- Вариационные ряды;
- Выборка;
- Корреляционный и регрессионный анализ;
- Ряды динамики.
Далее мы рассмотрим каждый из них более подробно. Но отметим, что представим лишь основные характеристики без подробного описания алгоритмов действий. Впрочем, понять их не составит никакого труда.
Статистическое наблюдение
Статистическое наблюдение является планомерным, организованным и в большинстве случаев систематическим сбором информации, направленным, главным образом, на явления социальной жизни. Реализуется данный метод через регистрацию предварительно определенных наиболее ярких признаков, цель которой состоит в последующем получении характеристик изучаемых явлений.
Статистическое наблюдение должно выполняться с учетом некоторых важных требований:
- Оно должно полностью охватывать изучаемые явления;
- Получаемые данные должны быть точными и достоверными;
- Получаемые данные должны быть однообразными и легкосопоставимыми.
Также статистическое наблюдение может иметь две формы:
- Отчетность – это такая форма статистического наблюдения, где информация поступает в конкретные статистические подразделения организаций, учреждений или предприятий. В этом случае данные вносятся в специальные отчеты.
- Специально организованное наблюдение – наблюдение, которое организуется с определенной целью, чтобы получить сведения, которых не имеется в отчетах, или же для уточнения и установления достоверности информации отчетов. К этой форме относятся опросы (например, опросы мнений людей), перепись населения и т.п.
Кроме того, статистическое наблюдение может быть категоризировано на основе двух признаков: либо на основе характера регистрации данных, либо на основе охвата единиц наблюдения. К первой категории относятся опросы, документирование и прямое наблюдение, а ко второй – наблюдение сплошное и несплошное, т.е. выборочное.
Для получения данных при помощи статистического наблюдения можно применять такие способы как анкетирование, корреспондентская деятельность, самоисчисление (когда наблюдаемые, например, сами заполняют соответствующие документы), экспедиции и составление отчетов.
Сводка и группировка материалов статистического наблюдения
Говоря о втором методе, в первую очередь следует сказать о сводке. Сводка представляет собой процесс обработки определенных единичных фактов, которые образуют общую совокупность данных, собранных при наблюдении. Если сводка проводится грамотно, огромное количество единичных данных об отдельных объектах наблюдения может превратиться в целый комплекс статистических таблиц и результатов. Также такое исследование способствует определению общих черт и закономерностей исследуемых явлений.
С учетом показателей точности и глубины изучения можно выделить простую и сложную сводку, но любая из них должна основываться на конкретных этапах:
- Выбирается группировочный признак;
- Определяется порядок формирования групп;
- Разрабатывается система показателей, позволяющих охарактеризовать группу и объект или явление в целом;
- Разрабатываются макеты таблиц, где будут представлены результаты сводки.
Важно заметить, что есть и разные формы сводки:
- Централизованная сводка, требующая передачи полученного первичного материала в вышестоящий центр для последующей обработки;
- Децентрализованная сводка, где изучение данных происходит на нескольких ступенях по восходящей.
Выполняться же сводка может при помощи специализированного оборудования, например, с использованием компьютерного ПО или вручную.
Что же касается группировки, то этот процесс отличается разделением исследуемых данных на группы по признакам. Особенности поставленных статистическим анализом задач влияют на то, какой именно будет группировка: типологической, структурной или аналитической. Именно поэтому для сводки и группировки либо прибегают к услугам узкопрофильных специалистов, либо применяют конкретные техники мышления.
Абсолютные и относительные статистические величины
Абсолютные величина считаются самой первой формой представления статистических данных. С ее помощью удается придать явлениям размерные характеристики, например, по времени, по протяженности, по объему, по площади, по массе и т.д.
Если требуется узнать об индивидуальных абсолютных статистических величинах, можно прибегнуть к замерам, оценке, подсчету или взвешиванию. А если нужно получить итоговые объемные показатели, следует использовать сводку и группировку. Нужно иметь в виду, что абсолютные статистические величины отличаются наличием единиц измерения. К таким единицам относят стоимостные, трудовые и натуральные.
А относительные величины выражают количественные соотношения, касающиеся явлений социальной жизни. Чтобы их получить, одни величины всегда делятся на другие. Показатель, с которым сравнивают (это знаменатель), называют основанием сравнения, а показатель, которой сравнивают (это числитель), называют отчетной величиной.
Относительные величины могут быть разными, что зависит от их содержательной части. Например, существуют величины сравнения, величины уровня развития, величины интенсивности конкретного процесса, величины координации, структуры, динамики и т.д. и т.п.
Чтобы изучить какую-то совокупность по дифференцирующимся признакам, в статистическом анализе применяются средние величины – обобщающие качественные характеристики совокупности однородных явлений по какому-либо дифференцирующемуся признаку.
Крайне важным свойством средних величин является то, что они говорят о значениях конкретных признаков во всем их комплексе единым числом. Невзирая на то, что у отдельных единиц может наблюдаться количественная разница, средние величины выражают общие значения, свойственные всем единицам исследуемого комплекса. Получается, что при помощи характеристики чего-то одного можно получить характеристику целого.
Следует иметь в виду, что одним из самых важных условий применения средних величин, если проводится статистический анализ социальных явлений, считается однородность их комплекса, для которого и нужно узнать среднюю величину. А от такого, как именно будут представлены начальные данные для исчисления средней величины, будет зависеть и формула ее определения.
Вариационные ряды
В некоторых случаях данных о средних показателях тех или иных изучаемых величин может быть недостаточно, чтобы провести обработку, оценку и глубокий анализ какого-то явления или процесса. Тогда во внимание следует брать вариацию или разброс показателей отдельных единиц, который тоже представляет собой важную характеристику исследуемой совокупности.
На индивидуальные значения величин могут воздействовать многие факторы, а сами изучаемые явления или процессы могут быть очень многообразны, т.е. обладать вариацией (это многообразие и есть вариационные ряды), причины которой следует искать в сущности того, что изучается.
Вышеназванные абсолютные величины находятся в непосредственной зависимости от единиц измерения признаков, а значит, делают процесс изучения, оценки и сравнения двух и более вариационных рядов более сложным. А относительные показатели нужно вычислять в качестве соотношения абсолютных и средних показателей.
Выборка
Смысл выборочного метода (или проще – выборки) состоит в том, что по свойствам одной части определяются численные характеристики целого (это называется генеральной совокупностью). Основной выборочного метода является внутренняя связь, объединяющая части и целое, единичное и общее.
Метод выборки отличается рядом существенных преимуществ перед остальными, т.к. благодаря уменьшению количества наблюдений позволяет сократить объемы работы, затрачиваемые средства и усилия, а также успешно получать данные о таких процессах и явлениях, где либо нецелесообразно, либо просто невозможно исследовать их полностью.
Соответствие характеристик выборки характеристикам изучаемого явления или процесса будет зависеть от комплекса условий, и в первую очередь от того, как вообще будет реализовываться выборочный метод на практике. Это может быть как планомерный отбор, идущий по подготовленной схеме, так и непланомерный, когда выборка производится из генеральной совокупности.
Но во всех случаях выборочный метод должен быть типичным и соответствовать критериям объективности. Данные требования нужно выполнять всегда, т.к. именно от них будет зависеть соответствие характеристик метода и характеристик того, что подвергается статистическому анализу.
Таким образом, перед обработкой выборочного материала необходимо провести его тщательную проверку, избавившись тем самым от всего ненужного и второстепенного. Одновременно с этим, составляя выборку, в обязательном порядке нужно обходить стороной любую самодеятельность. Это означает, что ни в коем случае не следует делать выборку только из вариантов, кажущихся типичными, а все другие – отбрасывать.
Эффективная и качественная выборка должна составляться объективно, т.е. производить ее нужно так, чтобы были исключены любые субъективные влияния и предвзятые побуждения. И чтобы это условие было соблюдено должным образом, требуется прибегнуть к принципу рандомизации или, проще говоря, к принципу случайного отбора вариантов из всей их генеральной совокупности.
Представленный принцип служит основой теории выборочного метода, и следовать ему нужно всегда, когда требуется создать эффективную выборочную совокупность, причем случаи планомерного отбора исключением здесь не являются.
Корреляционный и регрессионный анализ
Корреляционный анализ и регрессионный анализ – это два высокоэффективных метода, позволяющие проводить анализ больших объемов данных для изучения возможной взаимосвязи двух или большего количества показателей.
В случае с корреляционным анализом задачами являются:
- Измерить тесноту имеющейся связи дифференцирующихся признаков;
- Определить неизвестные причинные связи;
- Оценить факторы, в наибольшей степени воздействующие на окончательный признак.
А в случае с регрессионным анализом задачи следующие:
- Определить форму связи;
- Установить степень воздействия независимых показателей на зависимый;
- Определить расчетные значения зависимого показателя.
Чтобы решить все вышеназванные задачи, практически всегда нужно применять и корреляционный и регрессионный анализ в комплексе.
Ряды динамики
Посредством этого метода статистического анализа очень удобно определять интенсивность или скорость, с которой развиваются явления, находить тенденцию их развития, выделять колебания, сравнивать динамику развития, находить взаимосвязь развивающихся во времени явлений.
Ряд динамики – это такой ряд, в котором во времени последовательно расположены статистические показатели, изменения которых характеризуют процесс развития исследуемого объекта или явления.
Ряд динамики включает в себя два компонента:
- Период или момент времени, связанный с имеющимися данными;
- Уровень или статистический показатель.
В совокупности эти компоненты представляют собой два члена ряда динамики, где первый член (временной период) обозначается буквой «t», а второй (уровень) – буквой «y».
Исходя из длительности временных промежутков, с которыми взаимосвязаны уровни, ряды динамики могут быть моментными и интервальными. Интервальные ряды позволяют складывать уровни для получения общей величины периодов, следующих один за другим, а в моментных такой возможности нет, но этого там и не требуется.
Ряды динамики также существуют с равными и разными интервалами. Суть же интервалов в моментных и интервальных рядах всегда разная. В первом случае интервалом является временной промежуток между датами, к которым привязаны данные для анализа (удобно использовать такой ряд, например, для определения количества действий за месяц, год и т.д.). А во втором случае – временной промежуток, к которому привязана совокупность обобщенных данных (такой ряд можно использовать для определения качества тех же самых действий за месяц, год и т.п.). Интервалы могут быть равными и разными, независимо от типа ряда.
Естественно, чтобы научиться грамотно применять каждый из методов статистического анализа, недостаточно просто знать о них, ведь, по сути, статистика – это целая наука, требующая еще и определенных навыков и умений. Но чтобы она давалась проще, можно и нужно тренировать свое мышление и улучшать когнитивные способности.
В остальном же исследование, оценка, обработка и анализ информации – очень интересные процессы. И даже в тех случаях, когда это не приводит к какому-то конкретному результату, за время исследования можно узнать множество интересных вещей. Статистический анализ нашел свое применение в огромном количестве сфер деятельности человека, а вы можете использовать его в учебе, работе, бизнесе и других областях, включая развитие детей и самообразование.
Источник


